BERNARD MESA
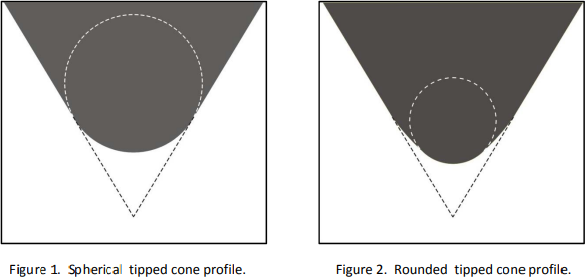
In the present field of nano indentation, spherical tipped indenters made of diamond or sapphire are desirable in numerous applications. A truly spherical tipped cone, as in Fig. 1, is difficult to fabricate at nanometer scale. In practice, a rounded cone may have a geometry similar to Fig. 2. The tip is spherical at the apex but has a transition section which is neither part of the sphere nor the cone. If only a minimal indentation depth is sufficient, such a rounded cone provides acceptable spherical indentations. When deeper indentations are needed, a more precise definition of the area function is required.
The analysis in the following pages offers a means to calculate the area function of rounded tip indenters with a single equation that is valid for both perfectly spherical and rounded cones.
First, the area function equations for the sphere, the cone and the spherical tipped cone are provided. Then the rounded cone equation and its application are described. The calculated area function values at regular indenting intervals are given in a spread sheet table.
Appendix A shows the equation derivation and Appendix B provides actual examples of rounded cone indenters analysis.
MST manufactures diamond and sapphire cone nano indenters with rounded tips at micrometer and nanometer dimensions. A TEM calibrated with a traceable standard is used to image and measure most of its nano indenters.
The graphic and calculated analysis of rounded conical indenters described here is available on request for purchased indenters. When ordering rounded cone indenters please supply the expected depth of indentation, in addition to the desired tip radius and cone angle.
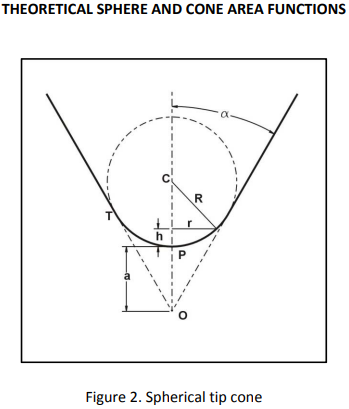
A cone indenter with a perfect spherical tip is shown on Fig. 2. The nomenclature used is as follows.
R Sphere radius
h Indentation depth
r Radius of projected circle at indentation depth
α Cone half angle
T Transition between cone and sphere
C Sphere center
P Indenter apex
O Cone theoretical apex
a Distance from P to O
An indenter area function f(h) allows the calculation of the projected area A of the circle of radius r at indentation depth h. Equation (2) is valid for all conical indenters which are assumed to have a circular symmetry.
r = f(h) (1)
A = π r2 (2)
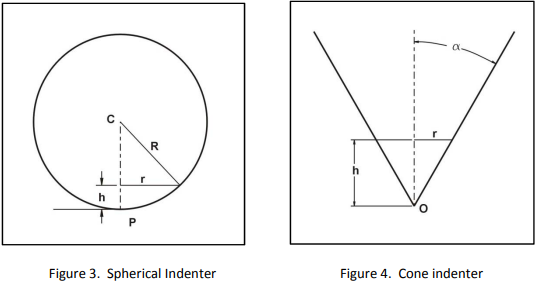
Simple spherical indenter equations,
r2 = R2 – (R‐h)2 (3)
r2 = 2Rh – h2 (4)
A = π (2Rh – h2) (5)
Simple conical indenter equations,
r = h tan α (6)
A = π h2 tan2 α (7)
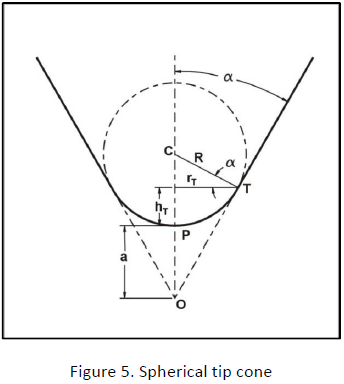
hT Indentation depth at the transition T between sphere and cone
rT Radius of projected circle at transition depth
Equations for the spherical section, when h ≤ hT:
r2 = 2Rh – h2 (4)
A = π (2Rh – h2) (5)
At the transition, when h = hT :
Sin α = (R – hT) / R (8)
hT = R (1 – Sin α) (9)
rT = R Cos α (10)
Equations for the conical section, when h ≥ hT:
Tan α = r / (a + h) (11)
r = Tan α (a + h) (12)
A = π [Tan α (a + h)]2 (13)
At the transition, when h = hT :
rT = Tan α ( a + hT ) (12)
Sin α = R / (R + a) (14)
a = R ( 1 / Sin α – 1 ) (15)
hT = R ( 1 – Sin α ) (9)
rT = Tan α [R ( 1 / Sin α – 1 ) + ( 1 – Sin α )] (16)
rT = R Tan α ( 1 / Sin α – Sin α ) (17)
rT = R ( 1 / Cos α – Sin2 α / Cos α ) (18)
rT = R [ 1– (1 – Cos2 α)] / Cos α (19)
rT = R Cos α (20)
Which is the same result for rT from the sphere:
rT = R Cos α (10)
ACTUAL ROUNDED CONE INDENTERS
Actual diamond nano indenters that approach a perfect spherical tip can only be made with considerable extra time and effort. There are two main reasons. One is the anisotropy of diamond which offers different abrasion rates at different crystal directions. This hampers circular symmetry.
The second reason is the very small dimensions required. At micro and nano meter scales the processes are not precise and repeatable enough to directly produce the desired geometries. These can only be approached by repeating the process in many small steps followed by measurements (usually with an electron microscope) until the required dimensions and tolerances are achieved.
Figs. 6, 7 and 8 show transmission electron microscope (TEM) images of three indenter examples. On the left is the plain TEM image. On the right some graphics have been superimposed. The larger circle indicates the sphere that would fit tangent to the cone sides. An spherical surface in this position would make the ideal spherical indenter.
The smaller circle is a closer approximation to the curve at the indenter tip. If the indentation depths are small in relation to the circle (less than 20% of the small circle radius), the indenter is acceptable as spherical. At deeper indentations the small circle radius would not be a good basis for accurate measurements.



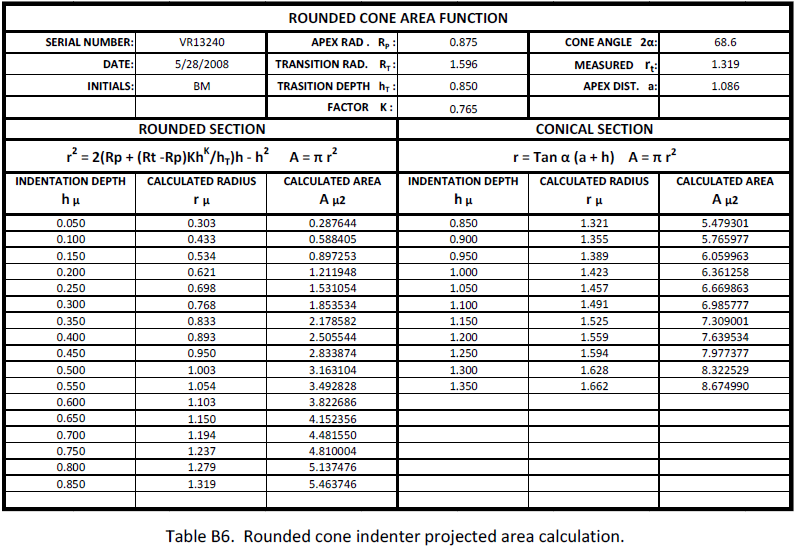
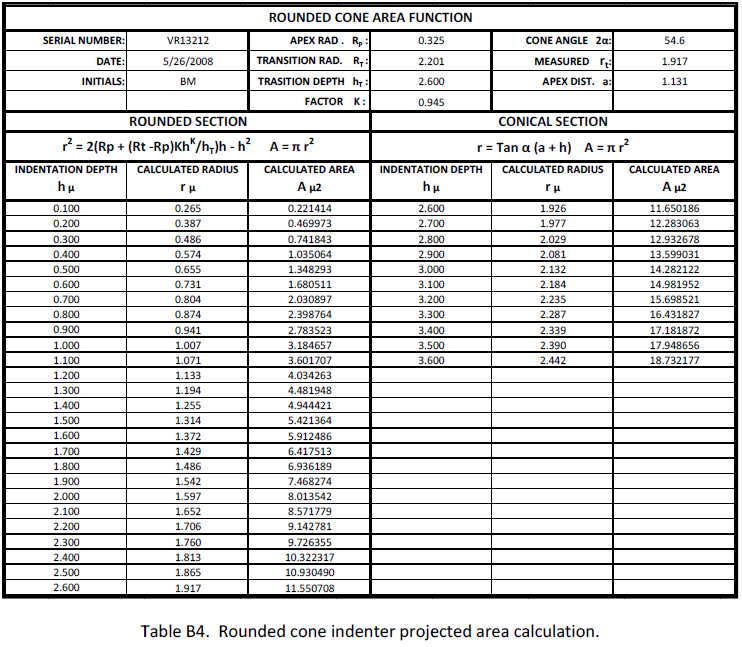
An investigation has been done on the non spherical geometry indenters to determine their area function general equation. There are two equations that provide the projected area as a function of the indentation depth. Equation (21) is applicable to the rounded section of the indenter and equation (12) to the conical section. Appendix A describes in detail the derivation of equation (21).
Radius of the projected circle at an indentation depth h, when h ≤ hT:
r2 = 2(RP + (RT ‐ RP) KhK / hT)h ‐ h2 (21)
Radius of the projected circle at an indentation depth h, when h ≤ hT:
r = Tan α (a + h) (12)
In both cases,
A = π r2 (2)
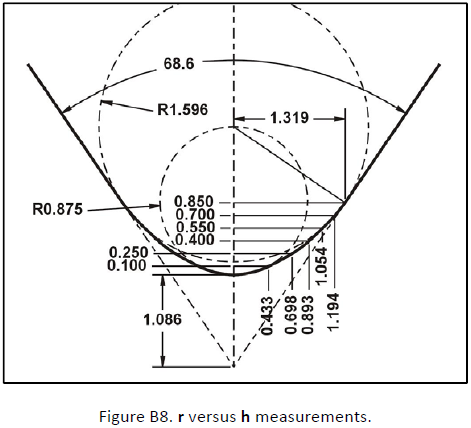
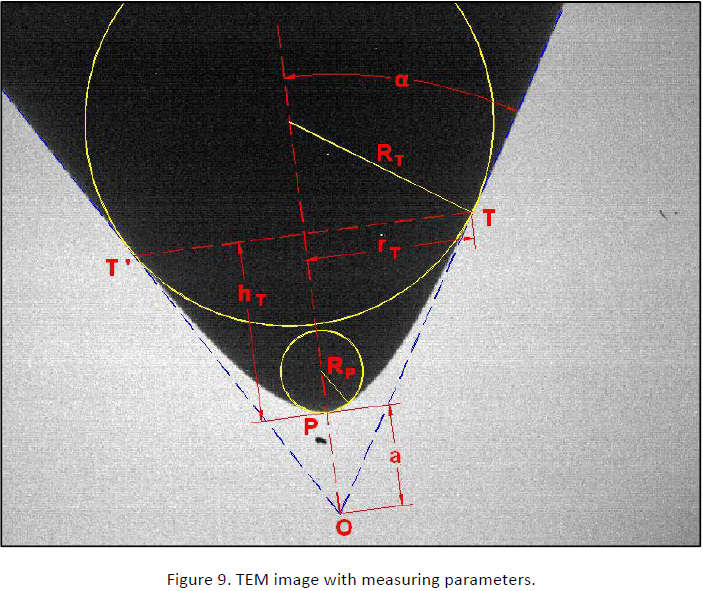
Fig. 9 shows the TEM image of indenter VR13211 with the measurement parameters required by equation (21). The two lines TO and T’O are the cone sides meeting at O. T is the transition where the tip’s curve starts. At point T a perpendicular line extended to the indenters center is the large circle radius or RT. The small circle radius RP is determined at a point where h is 2.5% of hT as explained on the Appendix. Following is the nomenclature for equation (21) and Fig. 9 not defined on page 2.
RP Apex circle radius
RT Transition point circle radius
hT Indentation depth at transition
rT Projected radius at transition depth
K Adjustable h coefficient and exponent.
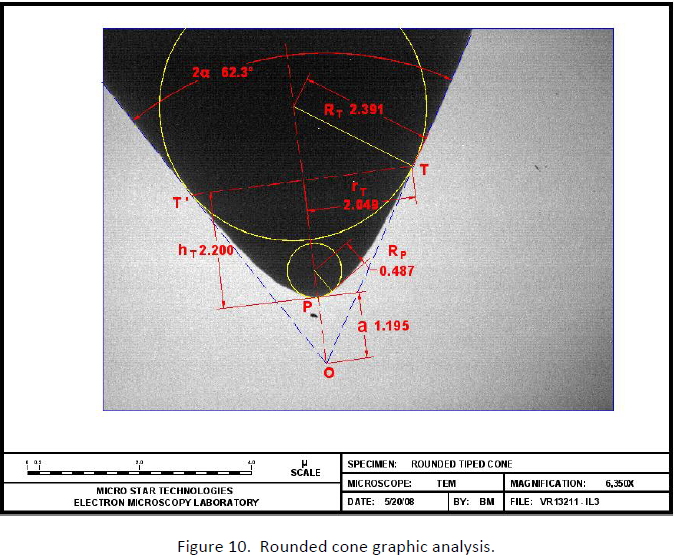
MST provides, on request, the analysis of a particular rounded cone indenter. For this purpose, the indenter’s TEM image is measured on a CAD program set to the microscope scale at which the image was taken. Fig. 10 shows the graphic analysis of indenter VR 13211 as an example.
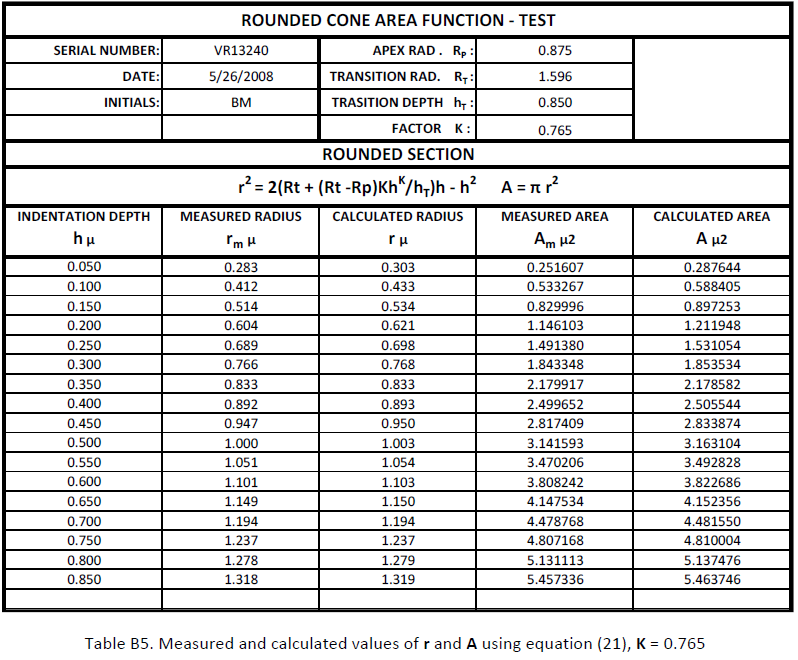
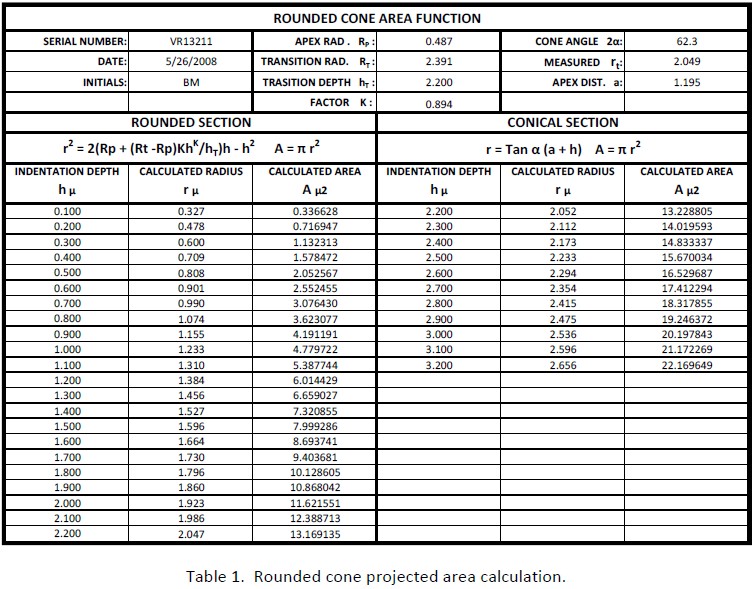
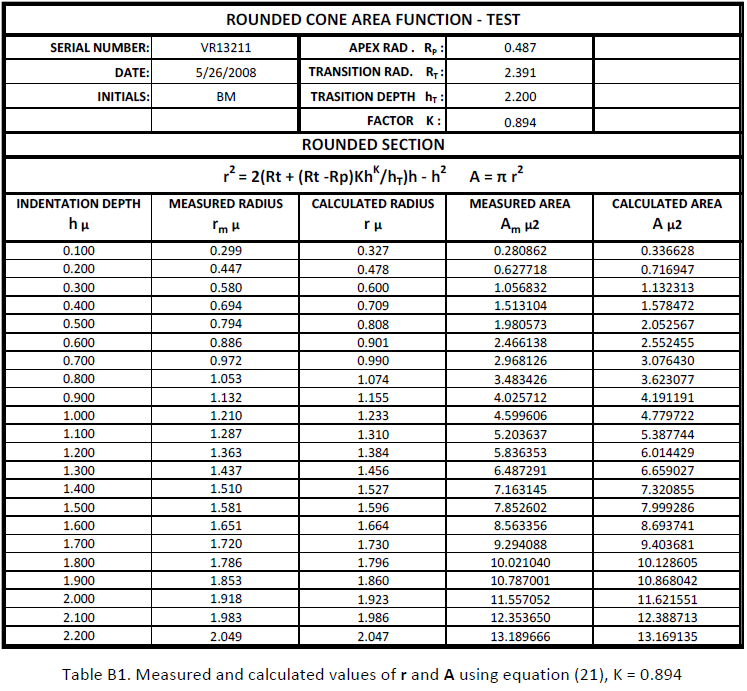
Table 1 is the spread sheet where the parameters have been entered. Equations (21 ) and (12) are used to calculate a series of values for r and A at equally spaced h intervals. Notice that rT (at h = hT = 2.200) is calculated independently with equations (21) and (12). The results differ slightly because the 3 significant decimal precision may round the values in some of the calculations.
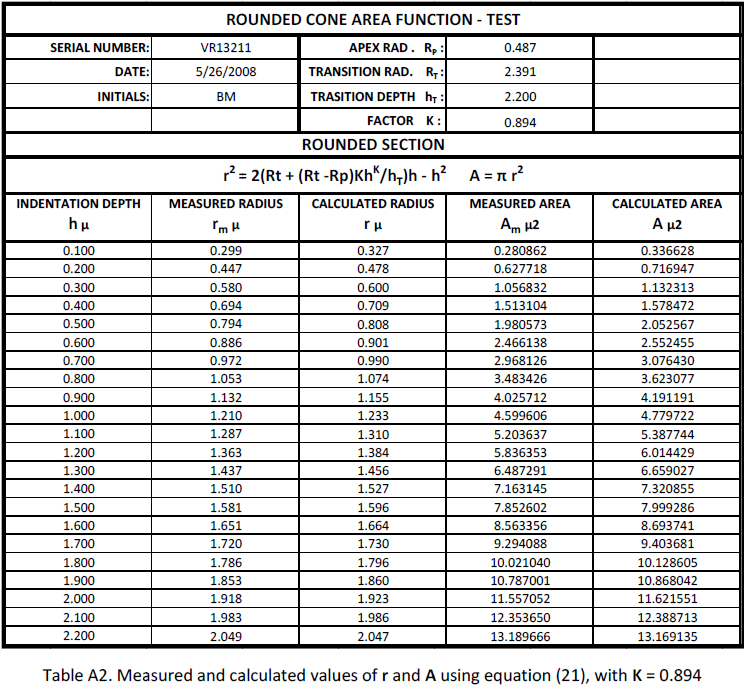
The “K factor” is a number used to adjust equation (21). K values fall between 1.00 and 0.70. The value of K is adjusted empirically to minimize the difference between rT calculated and rT measured. On Table 1 rT calculated with equation (21) is 2.047, rT measured is 2.049 using K = 0.890.
In the appendix several different indenters are measured point by point and compared to the calculated values, showing the validity of equation (21). In the case of a perfect spherical indenter RT = RP = R and, equation (21) becomes equation (4),
r2 = 2(RP + (RT – RP)KhK / hT)h – h2 = 2(R + (R – R)KhK / hT)h – h2 = 2Rh – h2 (4)
APPENDIX A
ROUNDED CONE AREA FUNCTION EQUATION DERIVATION
Consider the rounded cone indenter shown on Fig. A1. The rounded section curve starts at the transition point T. A circle of radius RT is drawn tangent to the cone at this point with the vertical distance to the apex P, hT. At a smaller distance from P, h3, another circle is drawn with radius R3. Similarly several more circles are drawn at h2, h1 and hP. The smallest circle conforms to the tip such that its radius RP is also valid at P when h = 0.
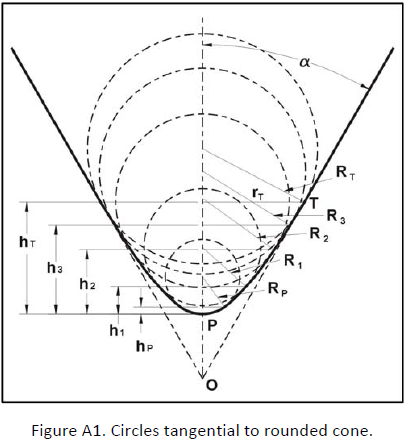
A perfectly spherical projection radius r is given by equation (4),
r2 = 2Rh – h2 (4)
This equation is not directly applicable to a rounded cone like in Fig. A1 because R is not a constant. It is apparent that the value of the radii Rn changes with the value of h. As the distance h gets larger the radii of the tangent circles also get larger. So R must be a function of h,
R = f(h) (A1)
From the rounded cone geometry the following corresponding values are found,
R = RP when h = 0 (A2)
R = RT when h = hT (A3)
A possible equation for R(h) could be,
R(h) = RP + Mh (A4)
RT = RP + MhT (A5)
M = (RT ‐ RP) / hT (A6)
R(h) = RP + (RT – RP)h / hT (A7)
And substituting in equation (4),
r2 = 2(RP + (RT – RP)h / hT)h – h2 (A8)
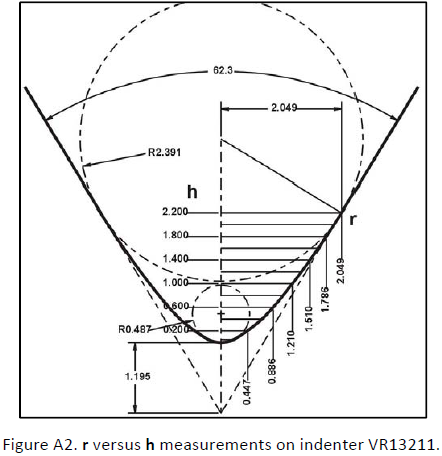
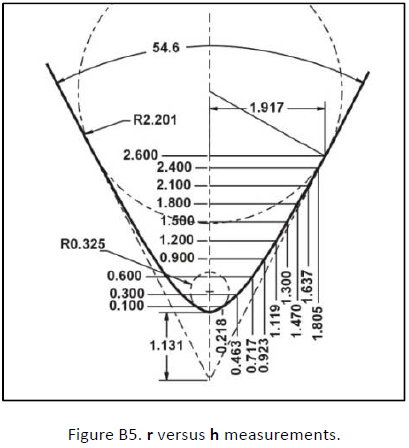
To test this equation, a careful measurement is made of the r values at equally spaced intervals of h on indenter VR13211 TEM image, as illustrated on Fig. A2 . For clarity, not all values are shown. All the measured values are inserted in Table A1.
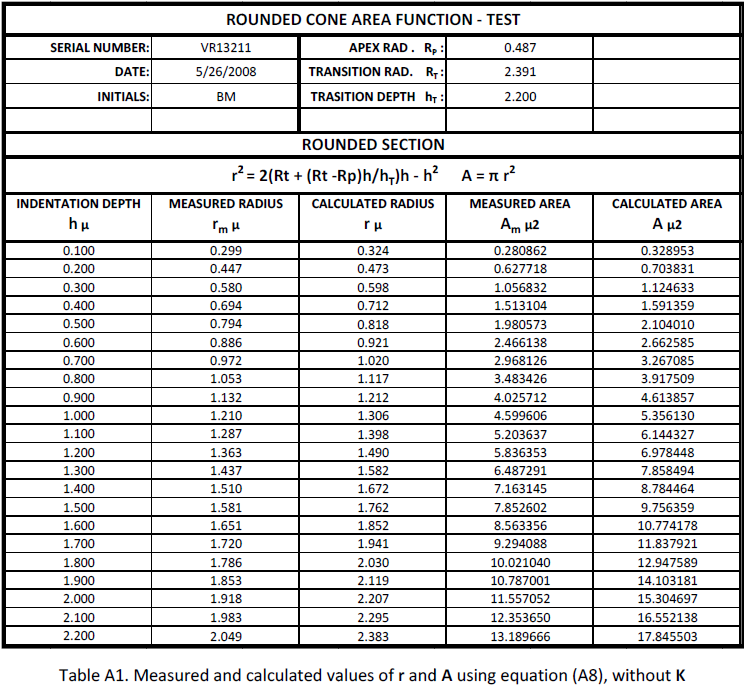
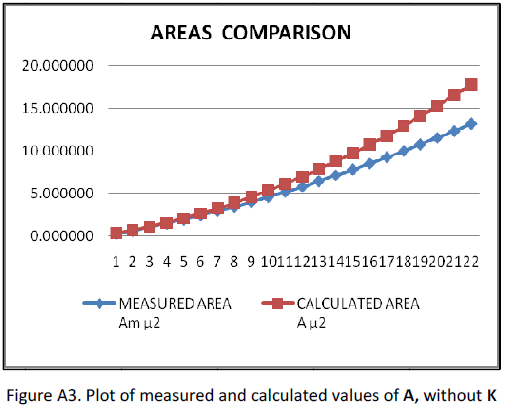
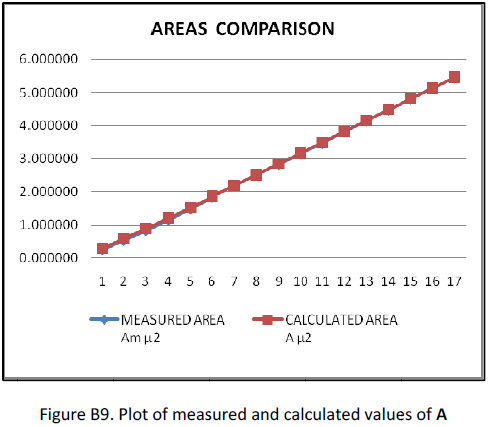
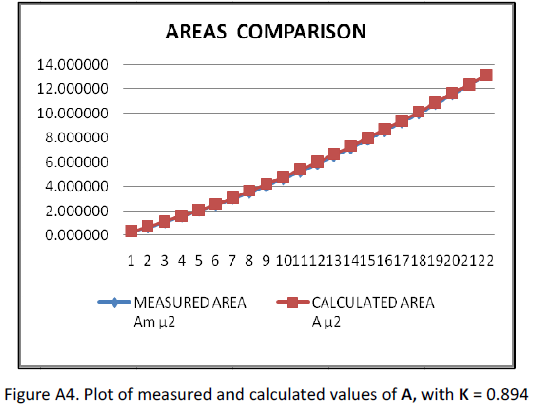
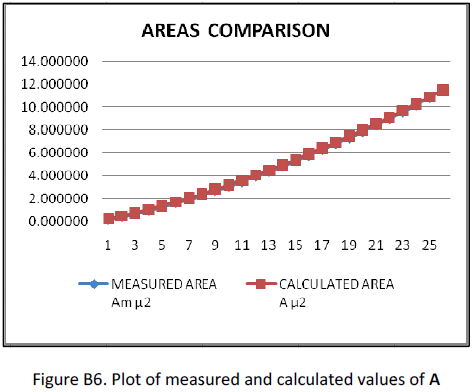
The calculated values of r and A on Table A1 are derived with equation (A8). Fig. A3 shows a plot comparison of the measured and calculated values of A. The divergence indicates that an equation to define R(h) for a rounded cone is not exactly linear as equation (A7). A modification was tried by adding a coefficient and exponent to h on equation (A9). Both were tested separately but it was found that their optimal values were similar. The same value, designated K, was chosen for exponent and coefficient,
R(h) = RP + (RT – RP)KhK / hT (A9)
r2 = 2(RP + (RT – RP)KhK / hT)h ‐ h2 (21)
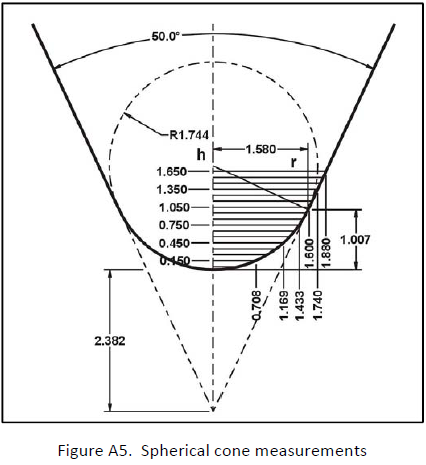
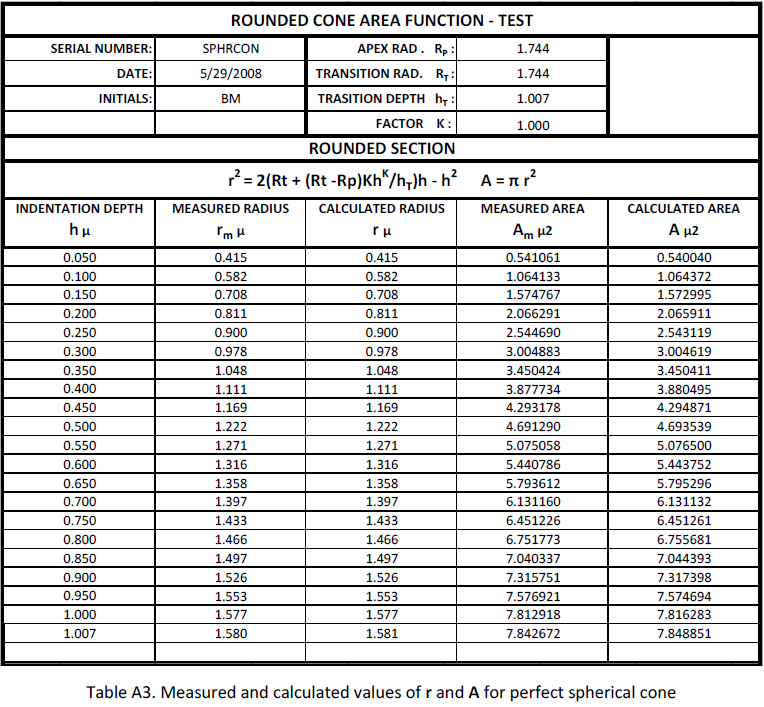
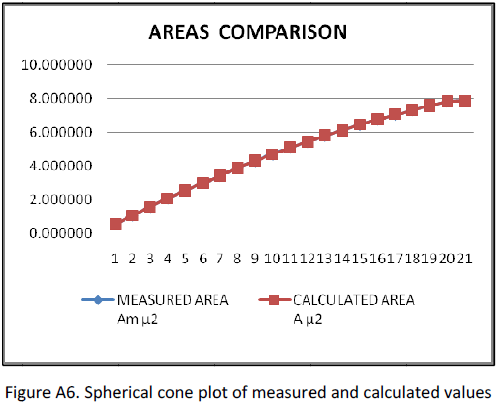
To confirm the validity of equation (21), a theoretical spherical cone is drawn on Fig. A5. The dimensions are tested on Table A3. Fig. A6 plots the comparison of measured and calculated values of A, which are identical. The value of K is irrelevant since (RT ‐ RP) = 0. Table A4 is the complete area function calculation for the spherical cone based on equations (21) and (22).
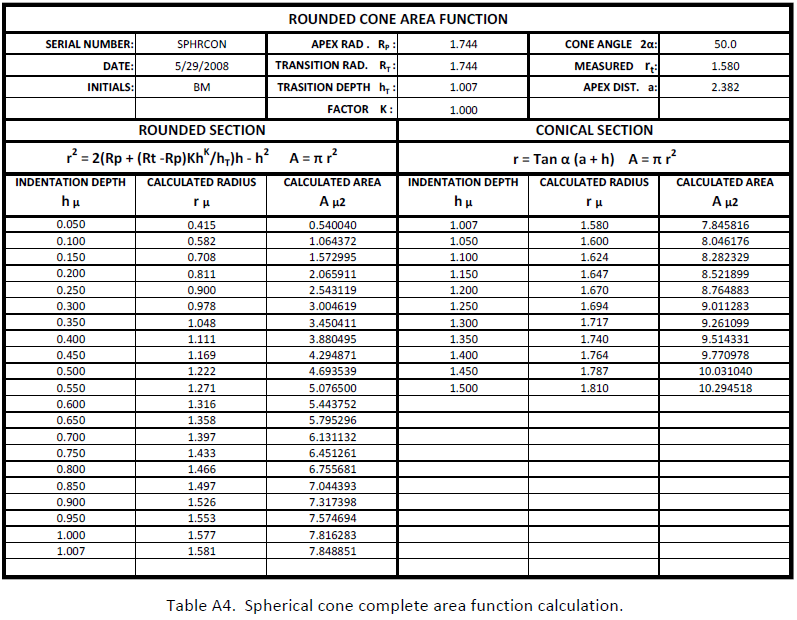
APPENDIX B
AREA FUNCTION EQUATION TESTS
Following is the complete set of data for three indenters analyzed with equation (21) and graphically measured to test the equation’s validity.
ROUNDED CONE INDENTER VR13211
The data is already presented in the previous pages but is repeated here for easier access.

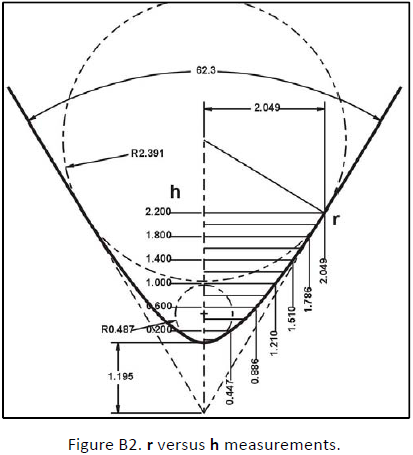
ROUNDED CONE INDENTER VR13211
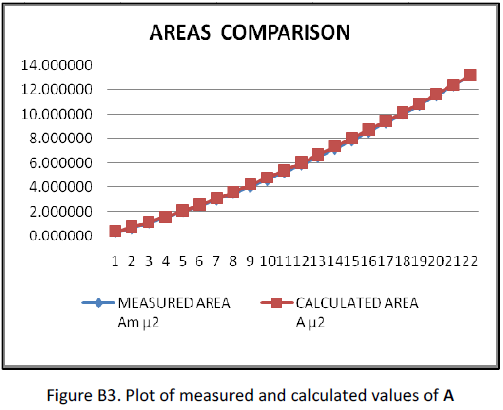
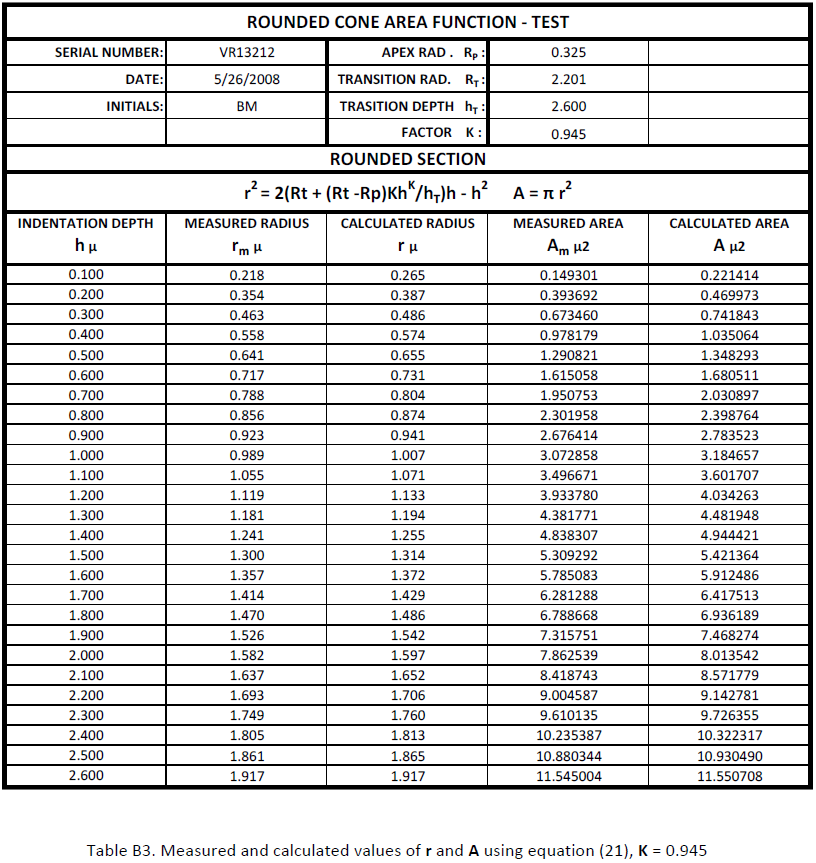
ROUNDED CONE INDENTER VR13212


ROUNDED CONE INDENTER VR13240